قانون مساحة متوازي المستطيلات

كتابة - آخر تحديث: ١٢:٤٤ ، ٦ أبريل ٢٠٢٠
قانون مساحة متوازي المستطيلات

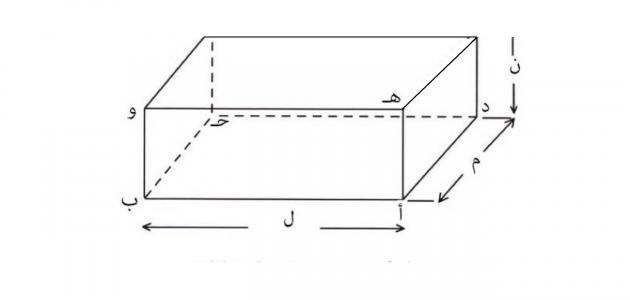
مساحة متوازي المستطيلات

يحتوي متوازي المستطيلات على ستة أوجه، ويمكن حساب مساحته من خلال إيجاد مجموع مساحات هذه الأوجه، ولكن بما أن الأوجه المتقابلة في متوازي المستطيلات متطابقة، فإننا نحتاج إلى ثلاثة أوجه فقط للتعبير عن المساحة، باستخدام الأبعاد الثلاثية للتعبير عنها، وهي: الطول، والعرض، والارتفاع، وذلك كما يلي:[١]

  • مساحة متوازي المستطيلات الكلية= (2×الطول×العرض) (2×العرض×الارتفاع) (2×الطول×الارتفاع)، وبالرموز: مساحة متوازي المستطيلات= (2×أ×ب) (2×ب×ع) (2×أ×ع)؛ حيث:
      • أ: طول متوازي المستطيلات.
      • ب: عرض متوازي المستطيلات.
      • ع: ارتفاع متوازي المستطيلات.


تجدر الإشارة هنا إلى أن أنه تم الضرب بالعدد 2؛ لأن كل وجهين متقابلين في متوازي المستطيلات متطابقان؛ أي لهما نفس المساحة، كما أن المساحة تُقاس بالوحدات الطولية المربعة.[١]


لمزيد من المعلومات والأمثلة حول متوازي المستطيلات يمكنك قراءة المقالات الآتية: تعريف متوازي المستطيلات.


المساحة الجانبية لمتوازي المستطيلات

تعرف المساحة الجانبية لمتوازي المستطيلات (بالإنجليزية: Cuboid Lateral Surface Area) بأنها مجموع مساحات الأوجه جميعها ما عدا الوجهين العلوي، والسفلي، ويمكن استخدام الصيغة الآتية لإيجاد المساحة الجانبية:[٢]

  • المساحة الجانبية لمتوازي المستطيلات = مساحة الأوجه الأربعة لمتوازي المستطيلات = 2 ×( العرض × الارتفاع) 2 × (الارتفاع × الطول)، وبإخراج الارتفاع كعامل مشترك، وترتيب الحدود فإن المساحة الجانبية تساوي: المساحة الجانبية لمتوازي المستطيلات= 2 × الارتفاع × (الطول العرض)، وبالرموز: المساحة الجانبية لمتوازي المستطيلات= 2 ×ع×(أ ب)؛ حيث:
      • أ: طول متوازي المستطيلات.
      • ب: عرض متوازي المستطيلات.
      • ع: ارتفاع متوازي المستطيلات.


أمثلة على حساب مساحة متوازي المستطيلات

  • المثال الأول: ما هي المساحة الكلية لصندوق على شكل متوازي المستطيلات طوله 6سم، وعرضه 5سم، وارتفاعه 4سم؟[٣]
    • الحل: يمكن إيجاد المساحة الكلية باتباع الخطوات الآتية:
      • مساحة متوازي المستطيلات = 2 × (الطول × العرض العرض × الارتفاع الارتفاع × الطول)= 2 × (6 × 5 5 × 4 4 × 6) = 2 × (30 20 24)= 2 × 74 = 148سم2.


  • المثال الثاني: ما هي المساحة الكلية لمتوازي المستطيلات الذي طوله 20سم، وعرضه 12سم، وارتفاعه 9سم؟[٤]
    • الحل: يمكن إيجاد المساحة الكلية باتباع الخطوات الآتية:
      • مساحة متوازي المستطيلات = 2 × (الطول × العرض العرض × الارتفاع الطول × الارتفاع)= 2 × ((20 × 12) (12 × 9) (20 × 9))= 2 × ( 240 108 180)= 2 × 528= 1056سم2.


  • المثال الثالث: ما هي المساحة الجانبية لمتوازي المستطيلات الذي طوله 3م، و عرضه 5م، وارتفاعه 4م؟[٤]
    • الحل: يمكن إيجاد المساحة الجانبية باتباع الخطوات الآتية:
      • المساحة الجانبية لمتوازي المستطيلات = 2 × الارتفاع × ( الطول العرض) = 2 × 4 × ( 3 5)
      • المساحة الجانبية = 8 × 8
      • المساحة الجانبية = 64م2.


  • المثال الرابع: ما هي المساحة الجانبية لمتوازي المستطيلات إذا كان طوله 12سم، وعرضه 13سم، وارتفاعه 15سم؟[٥]
    • الحل: يمكن إيجاد المساحة الجانبية باتباع الخطوات الآتية:
      • المساحة الجانبية لمتوازي المستطيلات = 2 × الارتفاع × ( الطول العرض)= 2 × 15 × ( 12 13)= 750سم2.


  • المثال الخامس: متوازي مستطيلات مساحته 40م2، ومساحته الجانبية 26م2، فما هي مساحة قاعدته؟[٦]
    • يمكن حل هذا السؤال باتباع الخطوات الآتية:
      • المساحة الكلية = 2 × مساحة القاعدة المساحة الجانبية، ومنه:
      • 40 = 2 × مساحة القاعدة 26، وبترتيب المعادلة بطرح (26) من الطرفين، ثم قسمتها على (2)، ينتج أن:
      • 2 × مساحة القاعدة = 14، ومنه: مساحة القاعدة = 7م2.
ملاحظة: تم ضرب مساحة القاعدة بالعدد 2 في هذا السؤال حتى تشمل القاعدتين العلوية، والسفلية.


  • المثال السادس: متوازي مستطيلات طوله 16سم، وعرضه 14سم، و ارتفاعه 10سم، فما هي مساحته الكلية؟[٧]
    • الحل: يمكن إيجاد المساحة باتباع الخطوات الآتية:
      • المساحة الكلية = 2 × (الطول × العرض العرض × الارتفاع الطول × الارتفاع)= 2 × (16 × 14 14 × 10 10 × 16)= 2 × (224 140 160)= 2 × 524= 1048سم2.


  • المثال السابع: متوازي مستطيلات مساحة قاعدته 20سم2، ومحيطها 20سم، فإذا كان ارتفاعه 6سم، فما هي مساحته الكلية؟[٨]
    • الحل: متوازي المستطيلات يتألف من قاعدتين، وأربعة وجوه، وبالتالي فإن مساحة متوازي المستطيلات =2 × (مساحة القاعدة) مساحة الأربع أوجه أو المساحة الجانبية، ومنه:
    • مساحة القاعدتين = 2 × مساحة القاعدة، وبالتالي: مساحة القاعدتين = 2 × 20= 40سم2.
    • مساحة الأربع وجوه أو المساحة الجانبية= 2 × الارتفاع × ( الطول العرض)، ولأن محيط القاعدة المستطيلة= 2 ×(الطول العرض)، فبالتالي المساحة الجانبية لمتوازي المستطيلات= محيط القاعدة× الارتفاع = 20 × 6= 120 سم2.
    • ومنه: مساحة متوازي المستطيلات = 120 40= 160 سم2.


  • المثال الثامن: صالة على شكل متوازي مستطيلات يُراد طلاء جدرانها الأربعة بالدهان فإذا كانت تكلفة المتر المربع الواحد 8 عملات نقدية، فما هي تكلفة طلاء جدران هذه الصالة بالدهان علماً أن محيط أرضها هو 250م، وارتفاعها هو 6م؟[٩]
    • الحل: تكلفة الطلاء = مساحة الجدران× تكلفة المتر المربع الواحد
    • يمكن حساب مساحة الجدران من خلال حساب المساحة الجانبية لمتوازي المستطيلات، وذلك كما يلي:
      • المساحة الجانبية = 2 × الارتفاع × (الطول العرض)
      • يمكن إيجاد 2 × (الطول العرض) من خلال المحيط؛ حيث إن المحيط يساوي 2 × (الطول العرض)، ويساوي 250م؛ وذلك لأن جميع أوجه متوازي المستطيلات تكون على شكل مستطيل، ومحيط المستطيل = 2 × (الطول العرض).
      • بالتعويض في قانون المساحة الجانبية فإن المساحة الجانبية = 6×250=1500م2.
    • تكلفة الدهان = 1500×8=12,000 عملة نقدية.


  • المثال التاسع: متوازي مستطيلات مساحته الكلية 214سم2، وحجمه 210 سم3، ومساحة قاعدته 42سم2، فما هي أبعاده الثلاثة الطول، والعرض، والارتفاع؟[١٠]
    • لحل هذا السؤال يتم اتباع الخطوات الآتية:
    • يمكن حل هذا السؤال باستخدام القوانين الآتية:
      • المساحة الكلية لمتوازي المستطيلات= 2×(الطول×العرض العرض×الارتفاع الارتفاع×الطول)
      • حجم متوازي المستطيلات = الطول × العرض × الارتفاع
      • مساحة القاعدة = الطول × العرض، وذلك لأن القاعدة مستطيلة الشكل.
    • يمكن من خلال قانوني الحجم، والمساحة حساب الارتفاع، وذلك كما يلي:
      • مساحة القاعدة = 42= الطول × العرض، وبتعويض هذه القيمة في قانون الحجم ينتج أن:
      • حجم متوازي المستطيلات = 42 × الارتفاع=210، وبقسمة الطرفين على (42) ينتج أن الارتفاع = 5سم.
    • تعويض الارتفاع في قانون مساحة متوازي المستطيلات كما يلي: 2 × (42 العرض×5 5×الطول) = 214؛ وذلك لأن القيمة (الطول×العرض) تمثّل المساحة، وتساوي 42، وبقسمة الطرفين على (2)، ثم طرح (42) من الطرفين ينتج أن: العرض×5 5×الطول= 65، وبقسمة الطرفين على (5) ينتج أن: الطول العرض= 13.
    • أصبحت لدينا المعادلتان الآتيتان:
      • المعادلة الأولى: الطول العرض = 13
      • المعادلة الثانية: الطول × العرض = 42
      • وبعد حل هذه المعادلات بالتعويض، ينتج أن قيمتي الطول، والعرض هما: الطول = 6سم، والعرض = 7سم.


لمزيد من المعلومات والأمثلة حول حجم متوازي المستطيلات يمكنك قراءة المقالات الآتية: قانون حجم متوازي المستطيلات.


  • المثال العاشر: بركة سباحة على شكل متوازي مستطيلات طولها 20م، وعرضها 15م،، وعمقها هو 4م، جد تكلفة دهانها إذا كانت تساوي 20 عملة نقدية لكل متر مربع؟[٩]
    • الحل: تكلفة الطلاء = مساحة الجدران الجانبية× تكلفة المتر المربع الواحد
    • يمكن حساب مساحة الجدران من خلال حساب المساحة الجانبية لمتوازي المستطيلات، وذلك كما يلي:
      • المساحة الجانبية = 2 × الارتفاع × (الطول العرض)=2 × 4 × (20 15)=280م2.
    • حساب تكلفة الدهان = 280×20=5,600 عملة نقدية.


فيديو عن حجم ومساحة متوازي المستطيلات

للتعرف على هذا الشكل الهندسي تابع الفيديو:[١١]



المراجع

  1. ^ أ ب "What is a Cuboid? - Definition, Shape, Area & Properties", www.tutors.com, Retrieved 3-4-2020. Edited.
  2. ↑ "https://www.vedantu.com/maths/cuboid-and-cube", www.vedantu.com, Retrieved 3-4-2020. Edited.
  3. ↑ "Total Surface Area of a Cuboid", www.mathsteacher.com.au, Retrieved 3-4-2020. Edited.
  4. ^ أ ب "cuboids", www.onlinemath4all.com, Retrieved 3-4-2020. Edited.
  5. ↑ "Cube and Cuboid", byjus.com, Retrieved 3-4-2020. Edited.
  6. ↑ "A cuboid", www.toppr.com, Retrieved 3-4-2020. Edited.
  7. ↑ "Surface Area of a Cuboid", www.web-formulas.com, Retrieved 3-4-2020. Edited.
  8. ↑ "Surface Area of a Cuboid", brilliant.org, Retrieved 3-4-2020. Edited.
  9. ^ أ ب "A cuboide ", www.toppr.com, Retrieved 3-4-2020. Edited.
  10. ↑ "surface area of acuboid", www.topperlearning.com, Retrieved 3-4-2020. Edited.
  11. ↑ فيديو عن حجم ومساحة متوازي المستطيلات.
1,352 مشاهدة