محتويات
نظرة عامة حول المكعب وشبه المكعب
يُعرف المكعب (بالإنجليزية: Cube) بأنه أحد المُجسّمات الهندسية الثلاثية الأبعاد، وأبعاده هي (الطول، والعرض، والارتفاع)، ويتكوّن المُكعّب من ستة أوجه مربعة الشكل ومتساوية في المساحة، وبما أنّ جميع أضلاع المربع متطابقة، فإن طول المكعب=عرضه= ارتفاعه، كما أنّه يتكون من 12 حرفاً، و8 رؤوس ناتجة عن التقاء ثلاثة أحرف مع بعضها البعض، وجميع زواياه قائمة.[١]
لمزيد من المعلومات حول المكعب يمكنك قراءة المقالات الآتية: قانون مساحة المكعب، كيفية حساب حجم المكعب.
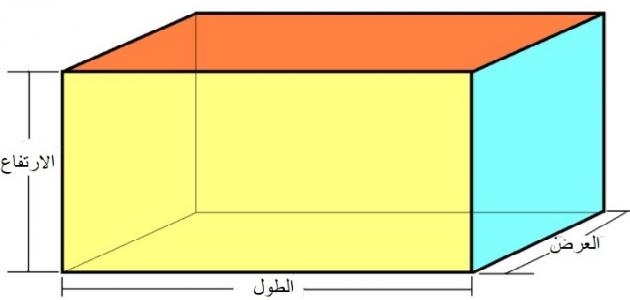
أما شبه المكعب فهو عبارة عن متوازي المستطيلات الذي يُعتبر أحد المجسمات الثلاثية الأبعاد، وقائمة الزوايا، وأبعاده الثلاثة هي: الطول، والعرض، والارتفاع، ويتكون شبه المكعب من ستة أوجه مستطيلة الشكل، كل وجهين منها متطابقان، وتتلاقى هذه الوجوه عند الأحرف، التي هي عبارة عن خطوط مستقيمة تلتقي كل ثلاثة منها في نقاط تُعرف باسم الرؤوس، ويختلف عن المكعب من ناحية أن وجوهه مستطيلة وليست متطابقة، كما أن أبعاده مختلفة وغير متساوية.[٢][٣]
لمزيد من المعلومات حول متوازي المستطيلات يمكنك قراءة المقال الآتي: تعريف متوازي المستطيلات.
قوانين شبه المكعب
- قانون مساحة شبه المكعب: يُعدّ شبه المكعب مُجسّماً متعدد الأوجه، ولحساب مساحته يجب حساب مجموع مساحات كل وجه من وجوهه المستطيلة الستة، وذلك كما يلي:[٤][٣]
- المساحة الكلية لشبه المكعب= مساحة أوجهه الجانبية مساحة القاعدتين = 2×(مساحة الوجه الأول) 2×(مساحة الوجه الثاني) 2×(مساحة الوجه الثالث) =2×(الطول×العرض) 2×(الطول×الارتفاع) 2×(العرض×الارتفاع)؛ علماً بأنّ قانون مساحة المستطيل= طول المستطيل× عرض المستطيل.
- مساحة شبه المكعب الجانبية=مساحة أوجهه الجانبية = 2×(الطول×الارتفاع) 2×(العرض×الارتفاع) = 2×الارتفاع×(الطول العرض)= محيط القاعدة (المستطيل)× الارتفاع؛ علماً أن: محيط المستطيل= 2×(طول المستطيل×عرض المستطيل).
لمزيد من المعلومات حول مساحة متوازي المستطيلات يمكنك قراءة المقال الآتي: قانون مساحة متوازي المستطيلات.
- قانون حجم شبه المكعب: يُعرف الحجم بشكل عام بأنه مقدار الفراغ الذي يملأ الشكل ثلاثي الأبعاد، ويمكن من خلال حساب حجم شبه المكعب حساب كمية الماء اللازمة لملء خزان ماء على شكل شبه مكعب مثلاً، وغيرها من الأمور، ويمكن حساب حجمه باستخدام العلاقة الآتية:[٤]
- حجم شبه المكعب= الطول×العرض×الارتفاع.
لمزيد من المعلومات والأمثلة حول حجم متوازي المستطيلات يمكنك قراءة المقالات الآتية: قانون حجم متوازي المستطيلات.
- قانون أقطار شبه المكعب: يمكن حساب طول أقطار شبه المنحرف باستخدام العلاقة الآتية:[٣]
- أقطار شبه المكعب = (الطول² العرض² الارتفاع²)√.
أمثلة متنوعة حول شبه المكعب
- المثال الأول: جد حجم ومساحة شبه المكعب إذا كان طوله 10سم، وعرضه 4سم، وارتفاعه 5سم.[٥]
- الحل:
- بالتعويض في القانون: حجم شبه المكعب= الطول×العرض×الارتفاع = 10×4×5 = 200 سم3.
- بالتعويض في القانون: مساحة شبه المكعب الكلية = 2×(الطول×العرض) 2×(الطول×الارتفاع) 2×(العرض×الارتفاع) = 2×(10×4) 2×(10×5) 2×(4×5) = 80 100 40 = 220 سم2.
- المثال الثاني: جد حجم ومساحة شبه المكعب إذا كان طوله 8سم، وعرضه 5سم، وارتفاعه 4سم.[٦]
- الحل:
- بالتعويض في القانون: حجم شبه المكعب= الطول×العرض×الارتفاع = 8×5×4 = 160 سم3.
- بالتعويض في القانون: مساحة شبه المكعب الكلية = 2×(الطول×العرض) 2×(الطول×الارتفاع) 2×(العرض×الارتفاع) = 2×(8×5) 2×(8×4) 2×(5×4) = 80 64 40 = 184 سم2.
- المثال الثالث: جد مساحة شبه المكعب الكلية والجانبية إذا كان طوله 10سم، وعرضه 8سم، وارتفاعه 7سم.[٧]
- الحل:
- بالتعويض في القانون: مساحة شبه المكعب الكلية = 2×(الطول×العرض) 2×(الطول×الارتفاع) 2×(العرض×الارتفاع) = 2×(10×8) 2×(10×7) 2×(8×7) = 160 140 112 = 412 سم2.
- بالتعويض في القانون: مساحة شبه المكعب الجانبية =2×(الطول×الارتفاع) 2×(العرض×الارتفاع) = 2×(10×7) 2×(8×7) = 140 112 = 262 سم2.
- المثال الرابع: جد طول أقطار شبه المكعب إذا كان طوله 15سم، وعرضه 9سم، وارتفاعه 6سم.[٨]
- الحل:
- بالتعويض في القانون: أقطار شبه المكعب = (الطول² العرض² الارتفاع²)√ = (15² 9² 6²)√ = 18.49 سم.
- المثال الخامس: إذا تم لصق أربعة مكعبات طول ضلع كل منها 4سم بجانب بعضها، لتكوّن شبه مكعب، جد تكلفة طلائه إذا كان ثمن طلاء السنتيمتر المربع الواحد منه 100عملة نقدية.[٨]
- الحل:
- لحساب تكلفة الطلاء يجب أولاً حساب المساحة الكلية لشبه المكعّب، ولحسابها يجب أولاً حساب طول ضلع أبعاد شبه المكعب، وذلك على النحو الآتي:
- طول شبه المكعب = 4× طول ضلع المكعب = 4× 4 =16سم.
- ارتفاع شبه المكعب = عرض شبه المكعب = طول ضلع المكعب =4سم.
- بتطبيق القانون: مساحة شبه المكعب الكلية = 2×(الطول×العرض) 2×(الطول×الارتفاع) 2×(العرض×الارتفاع) = 2×(16×4) 2×(16×4) 2×(4×4) = 128 128 32 = 288 سم2.
- حساب التكلفة الكلية لطلاء شبه المكعب: التكلفة الكلية = مساحة شبه المكعب× تكلفة الطلاء للسنتيمتر المربع الواحد = 288×100 = 28,800 عملة نقدية.
- المثال السادس: جد الكتلة الكلية لأربعة قضبان حديدية على شكل شبه مكعب إذا كان طول كل منها 0.2م، وعرضه 0.1م، وارتفاعه 0.6م، علماً أن كتلة السنتيمتر المكعب الواحد هي 8 غرامات.[٨]
- الحل:
- لحساب كتلة القضبان الحديدية يجب أولاً حساب حجمها، وذلك باستخدام القانون: حجم شبه المكعب= الطول×العرض×الارتفاع = 0.2×0.1×0.6 = 0.012 م3.
- تحويل الحجم من المتر المكعب إلى السنتيمتر المكعب، وذلك بضربه بالقيمة 1,000,000 ليصبح: 0.012×1,000,000 = 12,000 سم3.
- ضرب كتلة كل سنتيمتر مكعب بحجم شبه المكعب لحساب كتلة القضيب الحديدي الواحد: كتلة القضيب الواحد= 12,000× 8 = 96,000غ، كتلة القضبان الثمانية = 4×96,000 =384,000غ = 384كغ.
المراجع
- ↑ "Cube Hexahedron", www.mathsisfun.com, Retrieved 29-11-2017. Edited.
- ↑ "Cuboid", www.mathworld.wolfram.com, Retrieved 9-12-2017. Edited.
- ^ أ ب ت رجائي سميح العصار، جواد يونس أبو هليل، محمد زهير أبو صبيح (2013)، إلى أولمبياد ومسابقات الرياضيات (الطبعة الأولى)، الرياض: جامعة الملك فهد للبترول والمعادن عمادة البحث العلمي_مكتبة العبيكان، صفحة 85-90، جزء الأول. بتصرّف.
- ^ أ ب "What is a Cuboid Shape? - Definition, Area & Properties", www.study.com, Retrieved 9-12-2017. Edited.
- ↑ "Cuboids, Rectangular Prisms and Cubes", www.mathsisfun.com, Retrieved 9-12-2017. Edited.
- ↑ "Spinning Cube (Hexahedron) ", www.mathopolis.com, Retrieved 21-4-2020. Edited.
- ↑ "Surface Area of a Cuboid", www.web-formulas.com, Retrieved 21-4-2020. Edited.
- ^ أ ب ت Lata Wishram, UNDERSTANDING MATHEMATICS, Page 323. Edited.